Métodos públicos
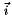 ,
, 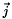 y
y 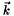 en el espacio 3D, define la correspondiente MATRIZ_4x4 de translación normalizada.
en el espacio 3D, define la correspondiente MATRIZ_4x4 de translación normalizada.
#include <matriz4.h>
Métodos públicos | |
| MATRIZ_4x4 () | |
| ~MATRIZ_4x4 () | |
| MATRIZ_4x4 | operator+ (MATRIZ_4x4 b) |
| (metodo revisado) | |
| MATRIZ_4x4 | operator * (MATRIZ_4x4 N) |
| Algoritmo de multiplicacion de matrices. | |
| VECTOR | operator * (VECTOR v) |
| OJO: Este metodo post-multiplica el vector de entrada `E` respecto a la matriz actual (M) y calcula asi el vector resultado `R` de la siguiente manera:. | |
| void | identidad (void) |
| MATRIZ_4x4 | inversa (void) |
| ATENCION: Solo las matrices cuadradas cuyo determinante es distinto de 0 tienen inversa! Como esta clase es de matrices de 4x4, las matrices son cuadradas (!)... | |
| double | determinante (void) |
| Calcula el determinante de la matriz. | |
| MATRIZ_4x4 | operator * (double a) |
| void | translacion (double transx, double transy, double transz) |
Dados los tres ángulos de translación sobre los vectores 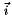 , , 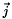 y y 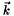 en el espacio 3D, define la correspondiente MATRIZ_4x4 de translación normalizada. en el espacio 3D, define la correspondiente MATRIZ_4x4 de translación normalizada. | |
| void | rotacion_eje (double angulo, double x, double y, double z) |
| Tomada del codigo de Mesa (Erich Boleyn - erich@uruk.org) (metodo revisado) ----------------------------------------------------------------------------- Arbitrary axis rotation matrix. | |
| void | rotacion_angulos_euler (double yaw, double pitch, double roll) |
| Dados tres angulos de rotacion, construye en esta matriz la correspondiente matriz de rotacion. | |
| void | rotacion_punto_punto (VECTOR p1, VECTOR p2) |
| Calcula la matriz de rotacion necesaria para convertir el vector <0, 0, 1> en un vector que va de p1 a p2. | |
| void | importar_quaternion (QUATERNION a) |
| Toma los datos del quaternion a (que es dela forma [a0, (a1, a2, a3)]) y lo convierte en una matriz. | |
| QUATERNION | exportar_quaternion (void) |
| Este metodo implementa la operacion inversa a `importar_quaternion`. | |
| void | exportar_angulos_euler (double *yaw, double *pitch, double *roll) |
| void | frustum (double plano_izquierdo, double plano_derecho, double plano_inferior, double plano_superior, double plano_cercano, double plano_lejano) |
| Este metodo implementa una funcion utilitaria para operaciones de visualizacion, y es equivalente a la operacion glFrustum de OpenGL. | |
| void | ortho (double plano_izquierdo, double plano_derecho, double plano_inferior, double plano_superior, double plano_cercano, double plano_lejano) |
| Este metodo implementa una funcion utilitaria para operaciones de visualizacion, y es equivalente a la operacion glOrtho de OpenGL. | |
| void | imprimir (void) |
| void | cargar_gl (void) |
| Este metodo multiplica la matriz de estado actual de OpenGL por la matriz de este objeto. | |
| void | importar_gl (void) |
| Este metodo importa la matriz actual de la maquina de estado virtual OpenGL, o en otras palabras, es la operacion complementaria a `cargue_gl`. | |
| void | activar_povray (FILE *fd) |
Atributos públicos | |
| double | M [4][4] |
La razon de esta "falta de generalidad" es que la eficiencia de las rutinas que manejan matrices de este tamaño es particularmente crítica para los algoritmos de visualización y simulación basada en física. Por lo tanto se recomienda usar esta matriz en lugar de versiones más genéricas, ya que aquí pueden encapsularse varias optimizaciones.
Esta clase es una perfecta candidata para usar las facilidades de aceleración de hardware de procesadores vectoriales y/o aceleradores gráficos. También es recomendable intentar probarla con metodos "inline" y todas las opciones de optimización que brinde el compilador.
Definición en la línea 29 del archivo matriz4.h.
|
|
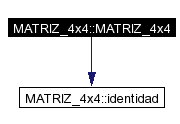
Definición en la línea 33 del archivo matriz4.C. References identidad(). |
Here is the call graph for this function:
|
|
|
|
|
Definición en la línea 611 del archivo matriz4.C. References M. Referenciado por COSA_RIGIDA::pintar_povray(). |
|
|
Este metodo multiplica la matriz de estado actual de OpenGL por la matriz de este objeto. Notese que la operacion `glMultMatrixd` recibe un arreglo que contiene una matriz en orden mayor de columna, es decir, que si el arreglo es {a0, a1, ..., a15}, se codifica la matriz: |a0 a4 a8 a12| | | |a1 a5 a9 a13| | | |a2 a6 a10 a14| | | |a3 a7 a11 a15| Lo cual no corresponde a la representacion interna de matrices AQUYNZA, que son de orden mayor fila. En concecuencia, este metodo utiliza un arreglo temporal `Mgl` compatible con la convencion OpenGL. OJO: - No olvide el glLoadIdentity de antes de esta funcion si lo que quiere es que OpenGL quede con esta matriz!
Definición en la línea 541 del archivo matriz4.C. Referenciado por CAMARA::activar_gl(), ESPACIO_ABIERTO::pintar_gl(), COSA_RIGIDA::pintar_gl(), CAMARA::pintar_gl(), ARTICULACION::pintar_gl(), VISOR_GEOMETRIA::pintar_nucleo_gl(), y PINTAR_VECTOR_GL(). |
|
|
Calcula el determinante de la matriz. OJO: Se esta calculando el determinante de una matriz de 3x3, no de una de 4x4! (metodo revisado) Definición en la línea 171 del archivo matriz4.C. References M. Referenciado por inversa(). |
|
||||||||||||||||
|
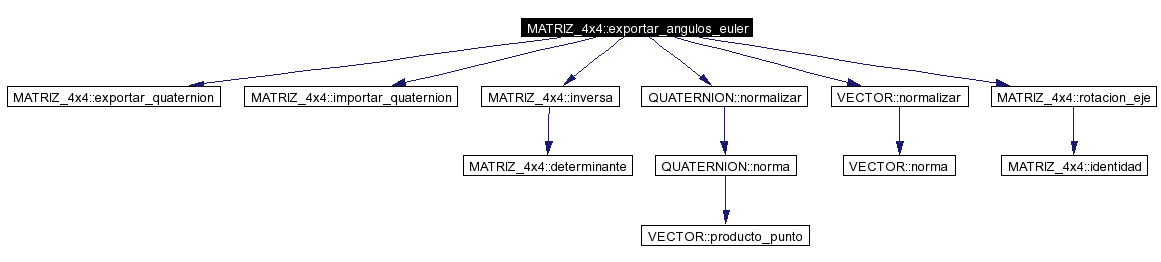
Definición en la línea 469 del archivo matriz4.C. References exportar_quaternion(), importar_quaternion(), inversa(), M, QUATERNION::normalizar(), VECTOR::normalizar(), rotacion_eje(), VECTOR::x, VECTOR::y, y VECTOR::z. Referenciado por COSA_RIGIDA::actualizar_variable(), COSA_RIGIDA::consultar_variable(), CONTROLADOR_DE_VUELO::ejecutar(), COSA_RIGIDA::grabar(), CAMARA::imprimir(), y BSP_2D::pintar_bsp(). |
Here is the call graph for this function:
|
|
Este metodo implementa la operacion inversa a `importar_quaternion`. Aunque no se exige, se espera que la matriz actual sea una matriz de rotacion. OJO: Este metodo no ha sido probado exhaustivamente! Definición en la línea 400 del archivo matriz4.C. References QUATERNION::direccion, M, QUATERNION::magnitud, VECTOR::x, VECTOR::y, y VECTOR::z. Referenciado por COSA_RIGIDA::actualizar_variable(), exportar_angulos_euler(), VISOR_GEOMETRIA::init(), VISOR_CAMPO_VECTORIAL::init(), LUZ::leer(), CAMARA::leer(), COSA_RIGIDA::leer_rigida(), LUZ::LUZ(), y COSA_RIGIDA::ODE_calcular_la_primera_derivada(). |
|
||||||||||||||||||||||||||||
|
Este metodo implementa una funcion utilitaria para operaciones de visualizacion, y es equivalente a la operacion glFrustum de OpenGL. La operacion define una matriz de proyeccion planar geometrica valida para ser usada en un volumen de visualizacion definido por la piramide truncada cuyo apex se encuentra en la posicion (0, 0, 0), y que se extiende hacia la direccion -z, con sus lados alineados a los ejes x y y. La superficie de proyeccion esta definida como el plano z = -plano_cercano, y la ventana de visualizacion (el viewport en coordenadas de la camara) se define en ese plano por los puntos extremos (plano_izquierdo, plano_inferior), (plano_derecho, plano_superior). Debe tenerse en cuenta que en algoritmos de tipo z-buffer, la presicion del valor de profundidad se afecta de manera indeseable de manera proporcional a la relacion (plano_lejano / plano_cercano). PRE: plano_cercano > 0 && plano_lejano > plano_cercano && plano_inferior < plano_superior && plano_izquierdo < plano_derecho. OJO: La precondicion no se verifica explicitamente. Si no se cumple, esta operacion puede conllevar a resultados inesperados. Definición en la línea 627 del archivo matriz4.C. References M. Referenciado por CAMARA::calcular_matriz_de_proyeccion(). |
|
|
Definición en la línea 92 del archivo matriz4.C. References M. Referenciado por COSA_RIGIDA::COSA_RIGIDA(), VISOR_GEOMETRIA::init(), MATRIZ_4x4(), COSA_RIGIDA::resolver_tensor_de_inercia(), y rotacion_eje(). |
|
|
Este metodo importa la matriz actual de la maquina de estado virtual OpenGL, o en otras palabras, es la operacion complementaria a `cargue_gl`. OJO: Notese que este metodo lee la matriz seleccionada actual, basandose en la configuracion del "GL_MATRIX_MODE" Para mayor informacion de los aspectos de conversion OpenGL/Aquynza, vea la documentacion del metodo `cargue_gl` de esta clase. Definición en la línea 582 del archivo matriz4.C. Referenciado por CAMARA::activar_gl(). |
|
|
Toma los datos del quaternion a (que es dela forma [a0, (a1, a2, a3)]) y lo convierte en una matriz. Si el quaternion es unitario (aunque no se exige, se espera que a este metodo le lleguen quaternions unitarios) la matriz resultante sera una matriz de rotacion. Para mayor informacion acerca de esta operacion, consulte en textos de matematicas el algebra de "quaternions", como extensiones a los numeros complejos en 4D, y que son utiles para realizar rotaciones en 3D. OJO: El funcionamiento de este metodo no ha sido probado exhaustivamente. No se sabe si su funcionamiento es "correcto". Definición en la línea 368 del archivo matriz4.C. References QUATERNION::direccion, M, QUATERNION::magnitud, VECTOR::x, VECTOR::y, y VECTOR::z. Referenciado por LUZ::activar_gl(), COSA_RIGIDA::actualizar_variable(), ESPACIO_ABIERTO::anexar_objetos_rayables(), CAMARA::calcular_matriz_de_proyeccion(), COSA_RIGIDA::consultar_variable(), exportar_angulos_euler(), COSA_RIGIDA::grabar(), CAMARA::imprimir(), ESPACIO_ABIERTO::interseccion(), COSA_RIGIDA::interseccion(), CAMARA::minmax_visible(), COSA_RIGIDA::ODE_calcular_la_primera_derivada(), BSP_2D::pintar_bsp(), ESPACIO_ABIERTO::pintar_gl(), COSA_RIGIDA::pintar_gl(), CAMARA::pintar_gl(), VISOR_GEOMETRIA::pintar_nucleo_gl(), COSA_RIGIDA::pintar_povray(), COSA_RIGIDA::posicion_absoluta(), CAMARA::preprocesar_vista(), CAMARA::procesar_mouse(), y COSA_RIGIDA::tensor_de_inercia(). |
|
|
Definición en la línea 524 del archivo matriz4.C. References M. Referenciado por CAMARA::activar_gl(). |
|
|
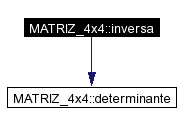
ATENCION: Solo las matrices cuadradas cuyo determinante es distinto de 0 tienen inversa! Como esta clase es de matrices de 4x4, las matrices son cuadradas (!)... PERO puede darse el caso de que el determinante sea 0... este metodo NO verifica el determinante de la matriz... luego se tiene: PRE: La matriz es invertible Notese que en AQUYNZA, las matrices que suelen invertirse son matrices de rotacion, las cuales SIEMPRE SON INVERTIBLES, dado que una matriz de rotacion representa una base de vectores ortonormales en R3 (consulte bibliografia en algebra lineal si aun no esta convencido). Sin embargo, asegurese del tipo de matrices que esta usando antes de tratar de invertirlas! Otro detalle para tener en cuenta: la inversa de una matriz que representa una base de vectores ortonormales tambien es una matriz de vectores ortonormales (!). OJO: SE ESTA CALCULANDO PARA MATRICES DE 3x3, NO PARA DE 4x4! (metodo revisado) Definición en la línea 121 del archivo matriz4.C. References determinante(), y M. Referenciado por LUZ::activar_gl(), ESPACIO_ABIERTO::anexar_objetos_rayables(), CAMARA::calcular_matriz_de_proyeccion(), exportar_angulos_euler(), FLECHA::interseccion(), ESPACIO_ABIERTO::interseccion(), COSA_RIGIDA::interseccion(), COSA_RIGIDA::ODE_calcular_la_primera_derivada(), COSA_RIGIDA::pintar_povray(), CAMARA::preprocesar_vista(), GIZMO_3D_TRANSLACION_3DSMAX::procesar_mouse(), y MANEJADOR_CONFLICTOS_COLISION::resolver_conflictos(). |
Here is the call graph for this function:
|
|
Definición en la línea 188 del archivo matriz4.C. References M. |
|
|
OJO: Este metodo post-multiplica el vector de entrada `E` respecto a la matriz actual (M) y calcula asi el vector resultado `R` de la siguiente manera:. |Rx| |M00 M01 M02 M03| |Ex| |Ry| = |M10 M11 M12 M13|*|Ey| |Rz| |M20 M21 M22 M23| |Ez| |Rw| |M30 M31 M32 M33| |Ew| Notese que es una multiplicacion en donde se usan VECTORES COLUMNA! Tengalo en cuenta a la hora de usar sus cosas... en particular, para las transformaciones geometricas compuestas, el orden en que se aplican las transformaciones es "de atras para adelante", por ejemplo, siguiendo el orden de numeracion 1..n, las trasformaciones Mi se ven: Mtotal = Mn * ... * M2 * M1 * M0 (metodo revisado) El metodo desactivado dentro de "NO_COMPILAR" ha sido utilizado para generar la version "ultra-optimizada" de ese metodo en linea. :-) |
|
|
Algoritmo de multiplicacion de matrices. Se retorna resultado = (*this) * segunda; (metodo revisado) Definición en la línea 66 del archivo matriz4.C. References M. |
|
|
(metodo revisado)
Definición en la línea 50 del archivo matriz4.C. References M. |
|
||||||||||||||||||||||||||||
|
Este metodo implementa una funcion utilitaria para operaciones de visualizacion, y es equivalente a la operacion glOrtho de OpenGL. PRE: plano_cercano > 0 && plano_lejano > plano_cercano && plano_inferior < plano_superior && plano_izquierdo < plano_derecho. OJO: La precondicion no se verifica explicitamente. Si no se cumple, esta operacion puede conllevar a resultados inesperados. Definición en la línea 684 del archivo matriz4.C. References M. Referenciado por CAMARA::calcular_matriz_de_proyeccion(). |
|
||||||||||||||||
|
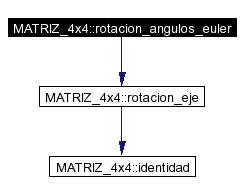
Dados tres angulos de rotacion, construye en esta matriz la correspondiente matriz de rotacion. OJO: El funcionamiento de este metodo no ha sido probado exhaustivamente. No se sabe si su funcionamiento es "correcto". En particular, se sospecha que, dado que esta idea funcione, no es nada eficiente... se propone investigar la matematica del asunto y aplicar eficiencia de algoritmos. Definición en la línea 219 del archivo matriz4.C. References rotacion_eje(). Referenciado por COSA_RIGIDA::actualizar_variable(), CONTROLADOR_DE_VUELO::ejecutar(), importar_3DS(), MESH::importar_obj(), VISOR_GEOMETRIA::init(), VISOR_CAMPO_VECTORIAL::init(), FLECHA::interseccion(), RAYO::leer(), LUZ::leer(), CAMARA::leer(), COSA_RIGIDA::leer_rigida(), GIZMO_3D_TRANSLACION_3DSMAX::procesar_mouse(), y rotacion_punto_punto(). |
Here is the call graph for this function:
|
||||||||||||||||||||
|
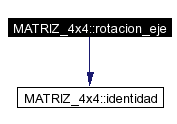
Tomada del codigo de Mesa (Erich Boleyn - erich@uruk.org) (metodo revisado) ----------------------------------------------------------------------------- Arbitrary axis rotation matrix. This is composed of 5 matrices, Rz, Ry, T, Ry', Rz', multiplied like so: Rz * Ry * T * Ry' * Rz'. T is the final rotation (which is about the X-axis), and the two composite transforms Ry' * Rz' and Rz * Ry are (respectively) the rotations necessary from the arbitrary axis to the X-axis then back. They are all elementary rotations. Rz' is a rotation about the Z-axis, to bring the axis vector into the x-z plane. Then Ry' is applied, rotating about the Y-axis to bring the axis vector parallel with the X-axis. The rotation about the X-axis is then performed. Ry and Rz are simply the respective inverse transforms to bring the arbitrary axis back to it's original orientation. The first transforms Rz' and Ry' are considered inverses, since the data from the arbitrary axis gives you info on how to get to it, not how to get away from it, and an inverse must be applied. The basic calculation used is to recognize that the arbitrary axis vector (x, y, z), since it is of unit length, actually represents the sines and cosines of the angles to rotate the X-axis to the same orientation, with theta being the angle about Z and phi the angle about Y (in the order described above) as follows: cos (theta) = x / sqrt ( 1 - z^2 ) sin (theta) = y / sqrt ( 1 - z^2 ) cos (phi) = sqrt ( 1 - z^2 ) sin (phi) = z Note that cos (phi) can further be inserted to the above formulas: cos (theta) = x / cos (phi) sin (theta) = y / sin (phi) ...etc. Because of those relations and the standard trigonometric relations, it is pssible to reduce the transforms down to what is used below. It may be that any primary axis chosen will give the same results (modulo a sign convention) using thie method. Particularly nice is to notice that all divisions that might have caused trouble when parallel to certain planes or axis go away with care paid to reducing the expressions. After checking, it does perform correctly under all cases, since in all the cases of division where the denominator would have been zero, the numerator would have been zero as well, giving the expected result. Definición en la línea 241 del archivo matriz4.C. References identidad(), y M. Referenciado por CAMARA::calcular_matriz_de_proyeccion(), CONTROLADOR_DE_VUELO::ejecutar(), exportar_angulos_euler(), BSP_2D::pintar_bsp(), CAMARA::procesar_mouse(), rotacion_angulos_euler(), y rotacion_punto_punto(). |
Here is the call graph for this function:
|
||||||||||||
|
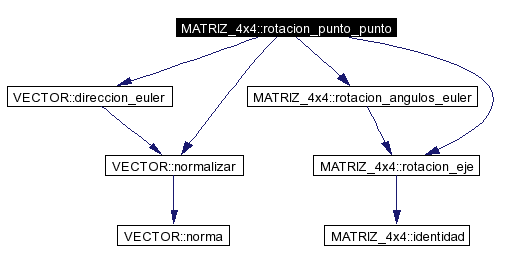
Calcula la matriz de rotacion necesaria para convertir el vector <0, 0, 1> en un vector que va de p1 a p2. Esto es util para pintar segmentos de recta solida en base a cilindros y cosas similares. Definición en la línea 344 del archivo matriz4.C. References VECTOR::direccion_euler(), VECTOR::normalizar(), rotacion_angulos_euler(), y rotacion_eje(). Referenciado por COSA_RIGIDA::aplicar_drag(), ARTICULACION::pintar_gl(), y PINTAR_VECTOR_GL(). |
Here is the call graph for this function:
|
||||||||||||||||
|
Dados los tres ángulos de translación sobre los vectores (método revisado) Definición en la línea 204 del archivo matriz4.C. References M. Referenciado por LUZ::activar_gl(), CAMARA::calcular_matriz_de_proyeccion(), CAMARA::minmax_visible(), CAMARA::pintar_gl(), y CAMARA::preprocesar_vista(). |
|
|
Definición en la línea 51 del archivo matriz4.h. Referenciado por activar_povray(), CAMARA::calcular_matriz_de_proyeccion(), cargar_gl(), determinante(), CONTROLADOR_DE_VUELO::ejecutar(), exportar_angulos_euler(), exportar_quaternion(), frustum(), identidad(), importar_gl(), importar_quaternion(), imprimir(), inversa(), operator *(), operator+(), ortho(), CAMARA::procesar_mouse(), COSA_RIGIDA::resolver_tensor_de_inercia(), rotacion_eje(), y translacion(). |